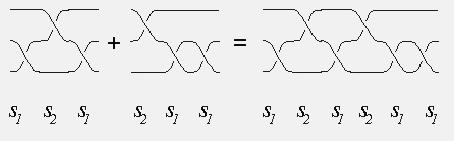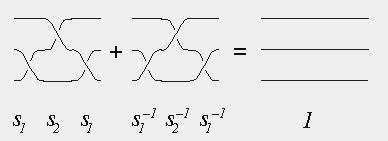A braid is a collection of strings connecting n fixed points with another set of n fixed points, as shown below. It is assumed the strings are monotone is some preferred direction, and two braids are considered equal if one can be deformed to the other through a continuous family of braids, with the endpoints fixed. Two braids on the same number of strings can be concatenated, forming their product.

The identity element of the group is the braid in which the strings are straight lines which do not intertwine at all. The inverse of a braid is its reflection in a mirror perpendicular to the preferred direction.

This multiplication gives the set of n-string braids the structure of a group, called B(n), which is non-commutative if n > 2. Emil Artin described this group in the 1920's and showed that is has generators s_j, 0 < j < n, which obey the rules

s_i s_j = s_j s_i     when   | i - j |   >  1
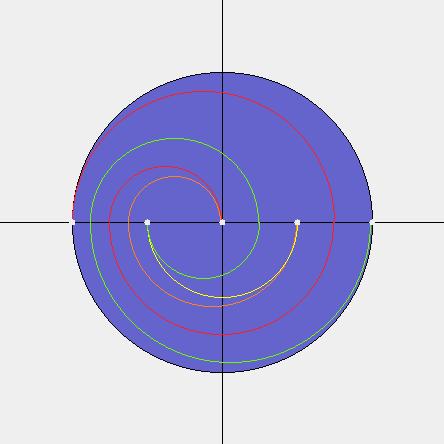
s_i s_j s_i = s_j s_i s_j     when   | i - j |  =  1.

PICTURE

By thinking of the preferred direction as "time", a braid may be regarded as the time history of n particles which move about in a plane, starting and ending at the same positions (but possibly permuted) and never colliding. The product of two such dances is just doing one dance after the other, and the identity braid is the "dance" in which nobody moves. The inverse of a dance is just doing the dance backwards in time. We customarily picture the starting and ending positions to be equally spaced points on a straight line (like the integers 1 through n lying on the real line, which in turn lies in the complex plane). The basic generator s_j is the little dance in which points j and j+1 exchange places, rotating clockwise (say), while the other dancers stay put.

PICTURE (ANIMATED?)

Imagining the plane (dance floor) to be made of rubber which sticks to the dancers as they twirl about. In this way, the motion of the points in a dance can extend to a continuous motion of the whole dance floor. The line, which started straight, at the end of the dance becomes a (possibly) very convoluted curve in the plane, which nevertheless visits each of the integer points, does not self-intersect, and is eventually straight (beyond the points 0 and n). This result is called a "curve diagram" for the dance, or for the braid. Conversely, given an abstract curve diagram with the above properties, one can imagine pulling it straight, like an elastic string, in the plane. The points 1 through n-1 will then perform a dance which is the inverse of the braid which gave rise to the curve diagram.

Just as different-looking braids may really be the same, different curve diagrams may correspond to the same braid. But up to the appropriate notions of equivalence, there is a one-to-one correspondence between braids and curve diagrams. The nice thing about curve diagrams is that there is a unique "canonical form" within each equivalence class. It is the diagram which has the smallest number of components of intersection with the straight line, consists of perfect semicircles in each half-plane above and below the straight line, possibly some straight line segments between adjacent starting points, and so that the curve passes through gaps between the points at equal intervals.

Given two braids, we look at their canonical curve diagrams. Following the diagrams from left to right, they will coincide for a while. But if the braids are different, their curve diagrams will also be different. Looking at the "first" point at which these curves diverge, one will turn left relative to the other. We will regard the one which turns left to be the greater of the two. It is not hard to see that this ordering is "invariant" under right multiplication: if a, b, c are braids with a < b according to this ordering, then we also have ac < bc. This is because, during the dance representing c, the diagrams of a and b will be moved in the same way, and their point of departure will look locally the same at the end of the dance. (However, ca might NOT be less than cb -- in fact it is impossible to find an ordering of braids, when n > 2, which is invariant under both right- and left-multiplication!) The braids which are greater than the identity braid, 1, are those whose canonical curve diagram departs first from the straight line in the upward direction. The APPLET can be used to compare braids a and b (given in terms of generators s_j) by using it to find the curve diagram for the product of a with the inverse of b (in that order). If it turns downward at its first departure from the straight line, then a < b. If it turns upward, a > b. If it goes straight across, a = b.

PICTURE (examples)

For more precise definitions, and proofs, please refer to the paper, "Ordering the Braid Groups," by Fenn, Green, Rolfsen, Rourke and Wiest, which may be downloaded from the site: http://xxx.lanl.gov/.